1.
(2017), mathematics is a discipline that has various areas of studies which relate with other discipline or subjects such as Basic Science, Basic technology and others which plays important role in the security, sustainability and technological development of any nation. In other words, mathematics is the linchpin in the task of technological development of any nation. Ale & Adetula (2010) highlights the intricate link of mathematics to science, and technology and opined that without the knowledge of mathematics, there would be no science, and without science, there will be no technology and without technology, there is no modern society.
Despite the importance accorded mathematic, it has been observed that students still perform poorly at T Author: Ph.D, National Mathematical Centre, Sheda-Kwali, Abuja, Nigeria. e-mail: [email protected] both internal and external examinations. The poor performance of students at the secondary school level has been a concern to the public in Nigeria. This is usually noticed when the yearly West African Senior School Certificate Examination (WASSCE) and Senior School Certificate Examination (SSCE) conducted by National Examination Council (NECO) results are released. This is evident in the performance of Nigerian candidates in general mathematics in the West African Secondary School Certificate Examination (WASSCE) from 2006 to 2011, which revealed that the percentage of students that passed mathematics at credit level was between 39% and 47%, except for a little improvement of 57.27% in 2008.
One of the factors attributed to the poor performance of students in mathematics achievement tests in schools as observed in literature is gender. There is the general belief that male students seem to perform better than female students in mathematics and mathematics-related subjects. According to Smith & Walker (1988) and Popoola & Ajani (2011), male students perform better than female students in mathematics. Etukudo (2002) opined that boys generally perform better than girls even though they are put into the same classroom situation. However, Cronbach (1977) was of the opinion that boys and girls do not differ much on ability measures. This is not unconnected with the fact that opportunities for development are much more the same until the school leaving age.
Multiple-choice is one of the various types of objective tests that can be used to measure learning outcomes; the score of the multiple-choice item is independent of the subjective influence of the marker or the examiner. Thus, the individual examiner doing the scoring is not required to make the judgment; the score is consistent regardless of the prejudice of the examiner. According to Barret (2001), multiple-choice tests are generally biased towards males, while the female students experience more difficulties with questions involving numerical, spatial, or high reasoning skills. It is generally believed that multiple-choice tests are prone to guessing. Thus, guesswork in most multiple-choice achievement tests has become the order of the day in most institutions. Ojerinde (1985) reported that in Nigeria, most students who do not have a flare for mathematics would result in guesswork at the secondary and tertiary levels. This is not unconnected with students testing their luck and thus gets out of the examination hall as quickly as possible. However, no statistics exist in this regard as to why students resort to guesswork, but if critically viewed within the test theories, it is assumed to be due to some psychological and situational factors.
Also, Lee, as cited in Adebule (2013), observed that questions always arise concerning whether high average test scores by certain groups are due to actual achievement differences, bias in test, or a combination of both. Conversely, the favored groups are the advantaged group during promotion and admission or selection into science-based courses in the high institutions while, the disadvantaged groups, on the other hand, are disallowed due to some factors tagged extraneous and irrelevant variables that interfere with the measurement of the underlying psychological construct being measured. These factors relate to the group like gender, socio-economic status, location has significant influence on the examinees' response to the item. This implies that the test is multidimensional or measures more than one trait.
Consequently, Smith (1985) referred to the above as measurement disturbance which was classified by Smith (1985) into three categories: 1. Disturbances as a result of characteristics of the person that is independent of the items such as fatigue, boredom, illness, cheating, among others. 2. Disturbances as a result of interaction between the characteristics of the person and the properties of the item, such as item content, item type, guessing, item bias, among others. 3. Disturbances as a result of the properties of the items which are independent of the characteristics of the person, such as the person's ability and item difficulty.
Many research findings have shown that there are differences in the academic performance of separate groups since the inception of testing. An item is biased if it discriminates between members of different groups who have the same ability on what is being measured. Put differently, members of different groups who have the same trait level differ in their score on the item. In his contribution, Plake, as cited in Adebule (2009), defines bias in tests as a situation when items in an achievement tests are found to favour one group over another for reasons not explainable by differences in achievement level between groups. Generally, bias in test items is regarded as a systematic error in measurement. Item bias is the degree to which items that comprise a measurement scale are systematically related to various exogenous variables (e.g., age, gender, location, race, and so on) after conditioning on the latent variable of interest. Items that show bias in any measuring instrument may affect the properties of the measuring instrument; for instance, test items that are for a group of equal ability should not have statistical differences between the groups. However, if differences exist between the groups, then the validity of the test items is threatened.
A test is gender-biased if men and women with comparable ability levels tend to obtain different scores. Thus, we can say that the test contained items that measure different traits for male and female examinees with comparable abilities. Test fairness is very important in test development; a test is said to be fair if systematic errors (biases) are not present. A systematic error occurs when the construct measured by a test contains some irrelevant elements that can threaten the validity of the test. A test should enable all examinees to have an equal chance to demonstrate personal skills and knowledge vital to the purpose of the test. Items that show bias in any measuring instrument may affect the properties of the measuring instrument. Thus, score generated from a test that contains items that are biased against one group or the other or test result from unfair testing procedures cannot be used to make a valid quality decisions in education.
Item response theory (IRT), also known as the latent trait theory or strong true score theory, is a family of latent trait models that are used to establish psychometric properties of items. According to Ojerinde, Popoola, Ojo, & Onyeneho (2012). Item response theory connotes and theoretically assumes that there exist a relatively common trait or characteristic that can be used to determine an individual's ability to succeed with a particular task. Such tasks may be in terms of the individual's response by thinking (cognitive), feeling (affective), and acting (psychomotor). This theory is considered to be one of the most important developments in psychological testing in recent times. Item response theory (IRT) model was designed to solve the problems of classical test theory (CTT); it has been the only theory that gives the valid measurement in terms of test construction and interpretation for assessment of test taker's ability in psychometric analysis. Many of the recent development in testing have their origin in the concept of IRT, such as tailored testing, adaptive computer testing, and improved equating of test forms. According to Pine (1977), Item bias based on the Item response theory (IRT) concept is classified as unbiased if all individuals having the same underlying trait (ability) have an equal probability of getting the item correct regardless of subgroup membership.
Differential item functioning (DIF), also referred to as measurement bias, exists when persons with different group membership but identical overall test scores have different probabilities of solving a test item correctly or giving a certain response on a Differential Item Functioning (DIF) occurs whenever people of the same ability level but different groups have different probabilities of endorsing an item. The focus of DIF analysis is on differences in performance between groups that are matched concerning ability, knowledge or skill of interest. Lee (1990) opined that to investigate bias at the item level, developers of large-scale assessments usually conduct a differential item functioning (DIF) analysis. However, not all cases of DIF necessarily have to be interpreted as item bias that will jeopardize the fairness of the test. Instead, DIF is a necessary but not sufficient condition for item bias. Thus, if DIF is not apparent for an item, then no item bias is present. However, if DIF is present, then its presence is not a sufficient condition to declare the item bias; rather one would have to apply a follow-up item bias analysis (e.g. content analysis, empirical evaluation) to determine the presence of item bias. For instance, if in a mathematics test, students of equal ability level from urban areas display a higher probability of answering an item correctly more than students from rural areas of equal ability level because the content in the test is biased against students from rural areas, then we say the item exhibit DIF and should be considered for modification or removal from the test items.
The Ondo State Joint Senior Secondary II Promotion Examination (OSJSSPE) was introduced as an intervention measure to reduce the poor performances of students in public examinations. It is only those students that passed the OSJSSPE both in public and private secondary schools that the state government would pay their registration fees and also allow them to sit for the West African Senior School Certificate Examination (WASSCE) and the Senior School Certificate Examination (SSCE) conducted by NECO in the Ondo State. The senior secondary II students that take these examinations are expected to have been exposed to the same course content at the same time frame within the same number of periods. Thus, they are supposed to be of equal probability of success irrespective of gender, location, and type of school.
The 2014 Ondo State Joint Senior Secondary II Promotion Examination (OSJSSPE) has undergone criticism from stakeholders in the education sector due to the failure rate, which was as bad as having less than half of the senior secondary II students in some schools promoted. Some critics believed that the state government, through the state functionaries in the ministry of education, influenced the result of the examination of the public schools to reduce the number of students in the Senior Secondary School III (SSS3), which will, in turn reduce the total amount to be paid to WAEC or NECO for registration by the state government through the ministry of education. The study investigated the differential item functioning (DIF) of all items in mathematics multiple-choice items of the 2015 Ondo State Joint Senior Secondary II Promotion Examination concerning the gender (male and female). The study was guided by the research question: What is the general performance of the students in the OSJSSPE multiple-choice mathematics items administered in 2015? Also, a Null hypothesis was postulated to guide the study; that is, the Ondo state Joint Senior Secondary II Promotion Examination (OSJSSPE) multiple-choice mathematics items administered in 2015 will not function differentially between males and female examinees.
2. II.
3. Research Method
The study adopted an ex-post-facto research design. For the ex-post facto design, the researcher started with the observation of the dependent variable and then studied the independent variables in retrospect for their possible relation to an effect on the dependent variable(s). This design is therefore relevant to this study because the researcher does not have direct control over the independent variables since the manifestations had directly occurred and the analysis would be performed on existing data. The population for the study consisted of 52,922 of male and female students in the senior secondary II that responded to the 50 multiplechoice items in mathematics of Ondo State Joint Senior Secondary II Promotion Examination (OSJSSPE) administered in 2015. The total sample for the study consisted of 3,135 senior secondary II students that responded to the 50 multiple-choice items in mathematics of OSJSSPE administered in 2015 as contained in the Optical Mark Recorder (OMR) sheets from twenty-four selected senior secondary schools in Ondo State, Nigeria, using two-stage sampling techniques. In the first stage, two local government areas (LGA) in each of the three senatorial districts of Ondo State were selected using the purposive sampling technique. In stage two, two public schools (one each from rural and urban areas) and two private schools (one each from rural and urban areas); thus, 12 public schools and 12 private schools were selected using a stratified sampling technique. A total of 24 schools were used for the study. The instruments used for the study were the responses of all the sampled students to the 50 multiple-choice items in mathematics of the OSJSSPE administered in 2015 in the selected schools as contained in the Optical Mark Recorder (OMR) sheets. The items were already subjected to the processes of validation and standardization by the examination Department of Ondo State Ministry of Education. Thus, they were already valid and reliable instruments.
The 50 multiple-choice items in mathematics which the students responded to and were used for this study was constructed, conducted, and administered by the Examination Department of the Ministry of Education in Ondo State. The OMR sheets comprised of section A and section B. Section A contains the demographic data of the respondents, while section B consisted of all items whose differential item functioning was determined. Descriptive statistics like percentages was used to answer the research question, while inferential statistics like the Welch t-test was used to test the hypothesis at a 0.05 level of significance.
4. III.
5. Results
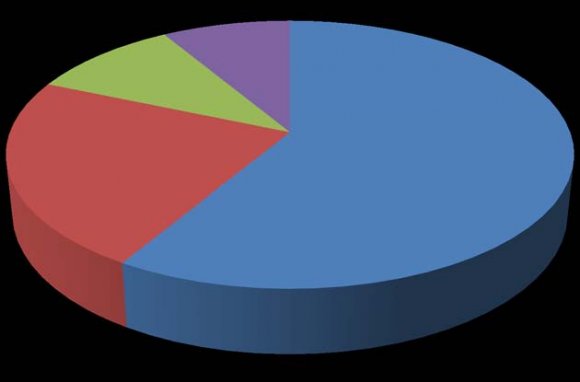
The results of the analysis are presented below. What is the general performance of students in the OSJSSPE multiple-choice mathematics items for 2015? Table 1 shows that 1686 (53.8%) of the students who sat for OSJSSPE had Distinction in Mathematics, 579 (18.5) had credit, 192 (6.1%) passed, while 678 (21.6%) failed. This implies that the General performance of the students in the OSJSSPE multiple-choice mathematics items for 2015 is high. The performance of the students in the OSJSSPE multiplechoice mathematics items for 2015 is further depicted in the figure below. A cursory look at Table 2 above shows that 28 (56%) items were flagged as DIF against both male and female examinees since their P value were less than 0.05. 13 items were flagged as DIF items against male examinees. The flagged items against male examinees are 8, 16,17,20,22,25,33,34,35,37,42,47 and 50. This is because their p -values are less than 0.05 in each case. Similarly, 15 items were flagged as DIF items against female examinees because their p-values are less than 0.05 in each case. The items that flagged as DIF items against female examinees are as follows: items 4,9,13,14,15,19,21,26,36,38,40,43,44,45 and 46 respectively. The study showed that 28 items listed above are statistically functioning differentially between males and females at the significance level of 0.05. The null hypothesis is rejected. This implies that the OSJSSPE multiple-Choice Mathematics items administered in 2015 function differentially between males and females examinees.
IV.
6. Discussion
The result showed that the general performance of the students in the OSJSSPE multiple-choice mathematics items administered in 2015 was high. The findings also revealed that 28 (56%) of the OSJSSPE multiple-choice mathematics items administered in 2015 displayed DIF based on the gender of the examinees using a statistically significant level of P-value of 0.05 (P < 0.05) (Linacre, 2010a). 13 items favoured male examinees while 15 items favoured the female examinees. The null hypothesis is rejected. This implies that the OSJSSPE multiple-choice mathematics items administered in 2015 functioned differentially between male and female examinees. This finding conforms with the finding of Adedoyin (2010) that mathematics items were gender-biased. Also, the result agrees with the findings of Banabas (2012) that mathematics questions used by WAEC contained items that measure different things for male and female examinees with the same mathematics ability. Abedalaziz (2010) and Madu (2012) also reported that mathematics items exhibit differential item functioning in favour of male examinees. However, the study contradicts Adebule (2013) that mathematics items did not function differentially based on the gender of the examinees.
V.
7. Conclusion
The study investigated items that exhibit differential item functioning in the 2015 Joint Senior Secondary II Mathematics Promotion Examination in Ondo State, Nigeria. Based on the findings, it was concluded that the general performance of the students in the OSJSSPE multiple-choice mathematics items administered in 2015 was high. Also, examinees of equal ability from both male and female students had a different probability of answering some items correctly; thus, the multiple-choice mathematics items of OSJSSPE administered in 2015 functioned differentially on male and female examinees.
8. VI.
9. Recommendations
Based on the findings, the following recommendations are made: 1) Examination bodies, Test experts, and people charged with developing, validating, and administering tests need to carry out differential item functioning analysis for all items before administration of a test.
2) There is a need for teachers, officials of the examination department in the ministry of Education to be trained by experts on item writing. This would acquit them with the processes of finding the psychometric properties and the detection of DIF of each item, which will, in turn, improve the quality of students' assessment in our schools. 3) Detection of DIF has been investigated using OSJSSPE multiple-choice mathematics items in this study. There is a need for replication using other cognitive subjects in OSJSSPE.
| Introduction |
| he importance of mathematics in the manpower |
| and technological development of a nation cannot |
| be overemphasized. According to Oloda and |
| Fakinlede |
| Academic Performance | N | 2015 | % | |
| Fail (0 -39) | 678 | 21.6 | ||
| Pass (40 -49) | 192 | 6.1 | ||
| Credit (50 -69) | 579 | 18.5 | ||
| Distinction (70 -100) | 1686 53.8 | |||
| Total | 3135 100.0 | |||
| Gender | male = 1 female = 2 | |||||||
| Item | Item | Joint | DIF | Rasch -Welch | ||||
| Numb | Name | S E | Contras | t | df | Prob | Bias Against | Decision |
| er 1 | I0001 | .11 | .19 | .19 | INF | .0729 | No DIF | |
| 2 | I0002 | .10 | -.03 | -.03 | INF | .7534 | No DIF | |
| 3 | I0003 | .11 | .00 | .00 | INF | 1.000 | Female | No DIF |
| 4 | I0004 | .10 | -.29 | -.29 | INF | .0045 | DIF | |
| 5 | I0005 | .10 | .00 | .00 | INF | 1.000 | No DIF | |
| 6 | I0006 | .10 | .00 | .00 | INF | 1.000 | Male | No DIF |
| 7 | I0007 | .10 | .15 | .15 | INF | .1605 | Female | No DIF |
| 8 | I0008 | .10 | .27 | .27 | INF | .0077 | DIF | |
| 9 10 11 12 13 14 | I0009 I0010 I0011 I0012 I0013 I0014 | .09 .09 .10 .10 .09 .10 | -.46 .00 .00 -.18 -.48 -.21 | -.46 .00 .00 -.18 -.48 -.21 | INF INF INF INF INF INF | .0000 1.000 1.000 .0703 .0000 .0340 | Female Female Female Male Male | DIF No DIF No DIF No DIF DIF DIF |
| 15 16 17 18 19 | I0015 I0016 I0017 I0018 I0019 | .10 .09 .09 .10 .09 | -.25 .21 .36 -.06 -.54 | -.25 .21 .36 -.06 -.54 | INF INF INF INF INF | .0117 .0177 .0000 .5396 .0000 | Female Male Female Male | DIF DIF DIF No DIF DIF |
| 20 21 22 | I0020 I0021 I0022 | .10 .10 .09 | .23 -.25 .59 | .23 -.25 .59 | INF INF INF | .0235 .0087 .0000 | Male Female | DIF DIF DIF |
| 23 | I0023 | .10 | .00 | .00 | INF | 1.000 | No DIF | |
| 24 | I0024 | .10 | -.12 | -.12 | INF | .2269 | No DIF | |
| 25 | I0025 | .09 | .32 | .32 | INF | .0004 | DIF | |
| 26 | I0026 | .09 | -.76 | -.76 | INF | .0000 | DIF | |
| 27 28 29 30 31 32 33 | I0027 I0028 I0029 I0030 I0031 I0032 I0033 | .10 .10 .09 .10 .10 .09 .10 | -.06 .12 .07 -.18 .00 .14 .44 | -.06 .12 .07 -.18 .00 .14 .44 | INF INF INF INF INF INF INF | .5236 .2319 .4365 .0642 1.000 .1286 .0000 | Male Male Male Female Male Female | No DIF No DIF No DIF No DIF No DIF No DIF DIF |
| 34 35 | I0034 I0035 | .10 .09 | .42 .92 | .42 .92 | INF INF | .0000 .0000 | Female | DIF DIF |
| 36 37 38 39 40 41 42 | I0036 I0037 I0038 I0039 I0040 I0041 I0042 | .10 .09 .10 .09 .09 .10 .10 | -,22 .36 -.27 .00 -.20 .12 .52 | -,22 .36 -.27 .00 -.20 .12 .52 | INF INF INF INF INF INF INF | .0268 .0001 .0062 1.000 .0257 .2148 .0000 | Male Female Female Female Female Male | DIF DIF DIF No DIF DIF No DIF DIF |
| 43 44 | I0043 I0044 | .09 .09 | -.57 -.22 | -.57 -.22 | INF INF | .0000 .0131 | Male | DIF DIF |
| 45 | I0045 | .10 | -.84 | -.84 | INF | .0000 | DIF | |
| 46 | I0046 | .10 | -.49 | -.49 | INF | .0000 | DIF | |
| 47 | I0047 | .09 | .62 | .62 | INF | .0000 | DIF | |
| 48 | I0048 | .10 | -.02 | -.02 | INF | .8247 | No DIF | |
| 49 | I0049 | .09 | -.14 | -.14 | INF | .1065 | No DIF | |
| 50 | I0050 | .10 | .61 | .61 | INF | .0000 | DIF | |