1. Vr?ac's Circles, Serbia
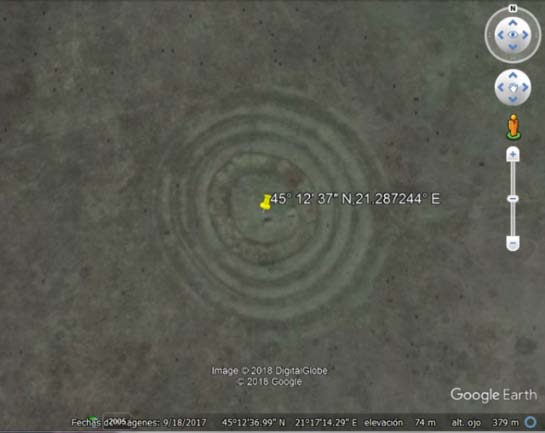
Abstract-Vr?ac Circles are a set of five, practically, concentric circles located in a plain of western Serbia. There have not been any systematic archaeological research in the zone but some exploration work indicate a possible date for the earthwork to be around five thousand years ago. In this paper, we present a sequential analysis of the sizes (diameters) of the circles that may obey, with the help of a gnomonic approach (the "gnomonic factor"), an algorithm involving the number of the circle and the height of the gnomon. The first assumption is that the smallest radius would be obtained from the shadow of a gnomon on winter solstice at noon; the others by the addition to the first a multiple of 1.5 times the gnomon's Introduction embers of the Association "Vla?i?i" for Archaeoastronomy and the Archaeoastronomical Society from Romania, made the trip to Vr?ac. The circular pattern they wanted to visit are five circles which centre is located at 45° 12' 37" N latitude and 21° 17' 14" E longitude. This unusual earthwork dated around five millennia ago can be seen in Figure 1. The aim of the trip was to exchange experiences and to formulate a joint work between both academic groups there. They had troubles to make the walk through the ancient Big Swamp of Vr?ac; after reaching the edge of the largest circle, the soil was not flat any more, and the can identify the five concentric circles: the larger with about 150m in diameter; the inner one just 50m or less. Several things were reported about this trip [1]. However, at the SEAC 2018 Conference that took place in Graz, Austria, part of the group met Raul, with whom they discussed some features on the collaboration done. The discussion arrived to the gnomonic factor [2] from which him exposed the importance to consider the shadows of a gnomon at solstices (winter and summer).
The present report covers one aspect of the collaboration that arise when exchanging data about Vr?ac Circles; the studies on the application of gnomonic factors (fg and fgp) to this site and the findings on the dimensions of the circles and their interpretation as a possible Calendrical Monument.
In the first part, a search for the significant values of the gnomonic factors is done: two main proposals come about when analysing the data. Then a study of the sizes (diameters) of the circles is made, discovering a special regularity. From this behaviour of radius and diameters, a possible gnomonic algorithm came apparent and its principal characteristics are presented in that section. These allow us to make some considerations on the possible origin and objectives of the circles, correlating them with a calendrical division of the year.
2. Possible Gnomonic Algorithm & Calendar from
From that meeting and the discussion that took place a possible collaboration become feasible. The fact of Latitude and its value of around 45° in the region of Serbia and Romania came later; the sites presented at the SEAC 2018 Conference by us would make relevant the issue because gnomons' shadow would be equal to its height. One of us (Marc) presented considerations about Sun alignments in the Neolithic times [3].
3. II.
4. The Gnomonic Factor search
The first step towards the evaluation of the possible influence of the gnomonic factor, fg, when the circles were designed, was to consider several suggested values for the Obliquity [1]. In Table 1, Gnomonic Factors at Vr?ac, the value of the factor expressed in decimal and as a fraction, are presented. As it can be seen easily, to values become of significant importance: 2 ¼ and 2 2/7.
I the last to rows of the table, the exact value of obliquity has been defined to obtain the exact decimal value of the fraction. In the previous to last row the exact value of 2.2500 or 2 ¼, for fg appears: The corresponding value of 24.0260 for obliquity implies an epoch of 3056 BC (using the Laskar algorithm to estimate it [4]). Then, our first proposal is that around the end of fourth millennia BC, the selection of the site to make the earthwork was made; specifically, a date around 3056 BC.
Due to the importance of the shadows of solstices at consideration the design of the circles could have took the observations of shadows. Here, a second consideration can be made. The definition of the radius of the smallest circle, the one which must have been defined in the first place, could arise from the measurement of the shadow of a gnomon at winter solstice (WSs). A measurement using Google Earth [5] gave us a diameter of 45.08m; thus a radius of 22.5405m could be assumed. In Table 1, a gnomon of 8.546m is suggested in order to get a WSs of that long Then, our second proposal is to consider a possible gnomon of 8.546m height located at the centre of the circles.
5. a) The Circles of Vr?ac
In a similar way, we have measured the diameter of the other four circles. The results of this operation are presented in Table 2, Diameters of Vr?ac's Circles, and the ratios between them and the smallest are reported also. One significant fact that must be enhanced here is the very similar values of the differences between successive diameters. The next step in our analysis was to consider the estimation of the ideal radius for each circle while considering the fractions reported in the last table, Table 2. In the following table, Table 3 Ideal Radius and Proportions for Circles, we recover the results for the analysis that can be summarized as follows: a) Five circles considered. We define the radius of the first circle as basis and numbered all of them from 1 to 5; b) Ideal radius. Using the fractions reported in Table 2, we calculate the ideal values of the circles going from 22.5405 to 72.1280; c) Differences. We calculate the differences between the radius and the corresponding one of first circle; and, d) Gnomon's fraction. We calculate how many times the gnomon height is in those differences.
Volume XVIII Issue II Version I The results appear very suggestive. The gnomon's fractions seem to be very regular: 1.5, 3.0, 4.5 and 6 times the gnomon, approximately. They could reflect a specific algorithm defined by the builders of the monument. Let's look forward to find a kind of procedure, possible, used around five millennia ago.
6. b) Gnomonic Algorithm
An analysis of Table 3, allows us to define the main characteristics of the algorithm that possibly was used to the design of the circles of Vr?ac. The radius of the circles seem to be equally separated and they appear to have a relation with the length of the gnomon.
7. c) Definition 1.Vr?ac's Algorithm
Using a gnomon, g, at Vr?ac, the radius, r n are the radius of the circles numbered with n=1, 2, 3, 4 and 5. The radius are calculated with the following expression:
r n =r 1 +(n-1)*b*g (1)Where r 1 is the WSs = 22.5405m and b is a constant equal to 1.5 or 1 ½, g = 8.546m.
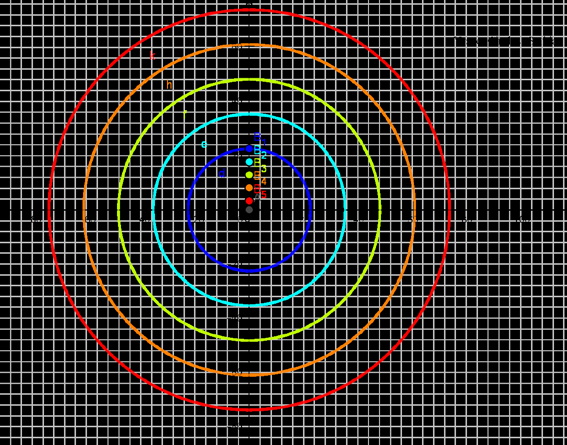
With this definition we have drawn the circles using Geo Gebra [6] and are shown in Figure 2. In it, a colour has been used in order to distinguish between them and for the reasons each of them will be apparent in the following section. In Figure 3, the five circles are shown overlapping the Google Earth image of the monument under analysis. It could be confirmed this way that the correspondence between the image and the drawing is almost in perfect harmony to the north-eastern quadrant of the figure.
Then, a new proposal could be given: it is possible that the design of the Vr?ac's Circles has been based on a simple algorithm including the use of a gnomon and the gnomonic factor.
8. On the image of Vrsac' Circles, Serbia
As it can be seen in the figure, there are marked in the south-north axis of the circles small points on the same colour as the circles. The Blue one corresponds to r 1 ; the light blue circle to the l-blue point, etc. This approach has to do with the other consideration appearing in Table 1: the size of the summer solstice shadow (SSs) that reaches the length of 3.3120m (red point). In next section, we suggest a further interpretation of the already presented results, in order to assimilate them in a calendrical context.
9. e) A Calendrical Design?
The Vr?ac's Circles is a well preserved monument. The locality has not been archaeologically explored. Only a shallow excavation was done and materials found suggested that the site was occupied at Neolithic times [1], our data goes in that direction for the dating. However, the probe on the ground has not been even clogged, gagging like a wound in the central circle.
Although not protected by anything, the formation of concentric circles is in a surprisingly good condition.
It seems to be protected by the remote location; the salty soil here is unsuitable for farming and the quick way of life of today's people no longer let them have time to walk around. Until about a hundred years ago it was protected by a swamp, now drained by relatively shallow canals. In spite of drainage, in several places it can be seen that the level of groundwater is high.In addition to this, the size of formation speaks in favor of Neolithic dating (similar Bronze Age circular formations are generally smaller).
Assuming a possible Neolithic design, we can ask about the reasons to build such a set of rings. Has it a relation with the religious ideas of the people? Or, was it more related to more quotidian issues like farming or chasing?
Our approach to the circles have found a relation between the winter solstice shadows of a possible great gnomon at the center. Then one can suggest that a kind of relation must be present for the other extreme shadow of the year: the summer solstice shadow.
10. f) Definition 2.Vr?ac's Shadows
The specified gnomon shadows (Gs) could be defined taking the differences in length of the solstices shadows (WSs, SSs, respectively) divided by 6 (g') (in a similar way as the circles), and then multiply by the fraction considered (b = 1 ½); i.e., s 1 = WSs = 22.5405m;
(
The results are shown in Table 4.
In the table we have calculated other values that will be discussed next. The fifth column of the Table 4, Sun_h (Sun's altitude), was calculated assuming that a gnomon (g = 8.546m) has to make a shadow of the corresponding length (Gs). This lengths are represented as coloured points in the already discussed Figure 2. These shadows appear in Figure 3. We have arrived to a kind of division of the year using the height of the Sun and the corresponding shadows of the gnomon. Using a sky simulator such as, for example Stellarium [7], one can verify the dates when the corresponding altitudes of the Sun were observed in the past. After an estimation of the #day and the lapses between each marked day, we can define a possible Vr?ac's Calendar with the dates of the year defining the principal days of a calendrical analysis. A Climatological analysis coming back to three millennia BC would help to feed with specific conditions the possible origin of this Vr?ac's Calendar and correlate them with the activities made by the people that constructed it. The colour of our circles in the drawing become meaningful: Blue for winter; light blue for cold/ice; Green for spring; orange for hot; and, Red for summer.
11. Volume XVIII Issue II Version I
12. III. Discussion and Conclusion
Our discussion on the definitions made around the design of the five circles found at Vr?ac´s site give us enough evidence to say that a kind of gnomonic design was involved there. The evidence pointing to the existence of an algorithm give us a tremendous task to try to confirm or disconfirm it. The mathematical abstraction that such a thinking implies could give support to other ideas about Neolithic world that have been suggested before [8].
Maybe a gnomon of 8.546m would be too high to set in position in the first place. Today, we have not any evidence of a work-earth at the site. Also, one must to assume that previous observations have to be made before the structure was made. Table 5, Scaling the Gnomon, shows that if a 1.899m gnomon is set at the desired point, the difference between solstices shadows is half the height of the final gnomon (obtained by us). A more credible size for the gnomon that possibly the people of Vr?ac (Vinca culture [9]) used to select the site and define the sizes of the circles.
13. Table 5: Scaling the Gnomon
This means that a gnomon of length 1.899m can explain the whole data of the site. Dividing this length by 6 one can expect to have a 0.3165m unit; maybe a unit called foot. The problem to this approach is that such a unit and a gnomon would not left any evidence for the long period that have elapse since.
Finely, we can suggest that the last table could confirms, precisely, that the site have been carefully selected and that the design obeyed a kind of gnomonic criteria; i.e., there was while designing the Vr?ac's Circles, a gnomonic algorithm that took into account the difference between solstices' shadows, more specifically, the possible use of the gnomonic factor became one of its foundations. Such an idea can contribute to the development of more detailed history of mathematics for that period.

![Figure 3: Overlap of the drawing of circles, generated with GeoGebra [4].](https://socialscienceresearch.org/index.php/GJHSS/article/download/101603/version/101603/1-Possible-Gnomonic-Algorithm_html/24286/image-5.png)
| Vr?ac | Serbia | |||||||||
| Lat | Lon | Epoch | ||||||||
| 45° 12? 37? | 21.287244 o | 3056 | BC | |||||||
| 45.21029 | 12.61758 | 37.0548 | ||||||||
| 90 | Gnomon | 8.546 | ||||||||
| Epoch | Oblqty | WS | SS | WSs | SSs | Fg | fg' | fgp | WSc | SSc |
| 24.200 | 20.5897 | 68.9897 | 2.661909 | 0.384070 | 2.2778 | 2 2/7 | 1.6619 | 22.7487 | 3.2822 | |
| 24.150 | 20.6397 | 68.9397 | 2.654890 | 0.385072 | 2.2698 | 2 1/4 | 1.6549 | 22.6885 | 3.2908 | |
| 24.100 | 20.6897 | 68.8897 | 2.647861 | 0.38607 | 2.2618 | 2 1/4 | 1.6479 | 22.6286 | 3.2993 | |
| 24.050 | 20.7397 | 68.8397 | 2.640887 | 0.387077 | 2.2538 | 2 1/4 | 1.6409 | 22.5690 | 3.3079 | |
| 24.000 | 20.7897 | 68.7897 | 2.633944 | 0.388081 | 2.2459 | 2 1/4 | 1.6339 | 22.5097 | 3.3165 | |
| 23.950 | 20.8397 | 68.7397 | 2.627033 | 0.389086 | 2.2379 | 2 1/4 | 1.6270 | 22.4506 | 3.3251 | |
| 23.900 | 20.8897 | 68.6897 | 2.620153 | 0.390091 | 2.2301 | 2 2/9 | 1.6202 | 22.3918 | 3.3337 | |
| 23.850 | 20.9397 | 68.6397 | 2.613310 | 0.391100 | 2.2222 | 2 2/9 | 1.6133 | 22.3331 | 3.3421 | |
| 23.800 | 20.9897 | 68.5897 | 2.606489 | 0.392103 | 2.2144 | 2 2/9 | 1.6065 | 22.2752 | 3.3509 | |
| 23.750 | 21.0397 | 68.5397 | 2.599703 | 0.393110 | 2.2066 | 2 1/5 | 1.5997 | 22.2171 | 3.3595 | |
| 23.700 | 21.0897 | 68.4897 | 2.592947 | 0.394118 | 2.1988 | 2 1/5 | 1.5929 | 22.1593 | 3.3681 | |
| -3056 | 24.0260 | 20.7637 | 68.816 | 2.637550 | 0.387559 | 2.2500 | 2 1/4 | 1.6376 | 22.5405 | 3.3120 |
| -7080 | 24.2330 | 20.5567 | 69.0227 | 2.666573 | 0.383410 | 2.2832 | 2 2/7 | 1.6666 | 22.7885 | 3.2766 |
| Diameter | Ratio | ratio_f | Diff |
| 45.08 | 1 | 1 0 | 27.37 |
| 72.45 | 1.60714286 | 1 3/5 | 25.05 |
| 97.50 | 2.16282165 | 2 1/6 | 23.08 |
| 120.58 | 2.67480035 | 2 2/3 | 23.24 |
| 143.82 | 3.19032831 | 3 1/5 |
| Circle Fraction | Ideal radius | Diff2 | Gnomon_f | |
| 1 | 1 | 22.540 | 0.000 | 0 |
| 2 | 1 3/5 | 36.064 | 13.524 1.58249473 | |
| 3 | 2 1/6 | 48.837 | 26.297 3.07707309 | |
| 4 | 2 2/3 | 60.107 | 37.567 4.39581871 | |
| 5 | 3 1/5 | 72.128 | 49.588 5.80248069 | |
| g | 3/8 | 8.546 | ||
| Shadow | Frac | Gs | Season | Sun_h | Day | #Day | Lapse | Calendar |
| 1 | 1 0 | 22.5405 | Winter | 20.764 | 12/01/-3056 | 0 | 21/dec | |
| 2 | 1 1/2 | 17.2964 | cold/ice | 26.294 | 20/02/-3056 | 39 | 39 | 29/jan |
| 3 | 3 0 | 12.3436 | Spring | 34.696 | 18/03/-3056 | 65 | 26 | 24/feb |
| 4 | 4 1/2 | 7.9735 | 46.985 | 20/04/-3056 | 98 | 33 | 29/mar | |
| 5 | 6 0 | 3.3121 | Summer | 68.816 | 17/07/-3056 | 186 | 88 | 25/jun |
| g' | 3.2366 | 46.985 | 10/10/-3056 | 271 | 85 | 18/sep | ||
| 34.696 | 09/11/-3056 | 301 | 30 | 18/oct | ||||
| 26.294 | 05/12/-3056 | 327 | 26 | 13/nov | ||||
| 20.764 | 12/01/-3055 | 365 | 38 | 21/dec |